حل معادله درجه سوم به روش خیام
حدود ۹۰۰ سال پیش، خیام روشی هندسی برای حل معادله ی درجه ی سوم به شکل:
x3+a2x=b , (b>=0)
ارائه کرد که در این جا به آن پرداخته ایم:
ابتدا یک سهمی به معادله ی x2=ay رسم می کنیم.
۲)دایره ای به قطر
AC=b/a2
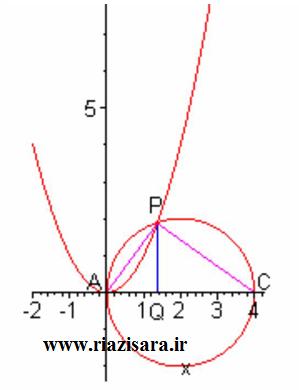
رسم می کنیم، به طوری که مرکز آن روی محور xها قرار داشته و دایره بر محور yها مماس باشد. (مانند آن چه که در شکل زیر آمده است.)
دایره ی رسم شده، سهمی را در نقطه ی P قطع می کند، از P عمودی برمحور xها رسم کرده و نقطه ی تقاطع را Q می نامیم.
اندازه ی پاره خط AQ ریشه ی معادله است.
اثبات: معادله ی دایره ی به مرکز
(b/2a2 , 0)
و شعاع
b/2a2
عبارت است از:
y2 + (x – b/(2a2))2 = b2/(4a2)
اگر این دایره را با سهمی
x2=ay
قطع دهیم به معادله ی
x3+a2x=b
می رسیم و این یعنی اندازه ی پاره خط AQ ریشه ی معادله ی درجه ی سوم مزبور است.