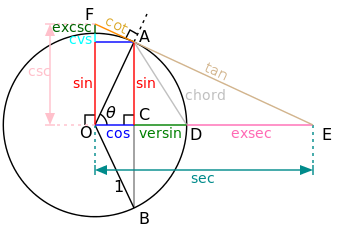
اتحادهای مثلثاتی مورد نیاز برای دانش آموزان

اتحادهای مثلثاتی

 

اتحادهای مثلثاتی

 

فهرستی از اتحادهای مثلثاتی (Trigonometric Identities):
 
 
 
\cos^2\theta + \sin^2\theta = 1\!
\sin\theta = \pm \sqrt{1-\cos^2\theta} \quad \text
\quad \cos\theta = \pm \sqrt{1 - \sin^2\theta} \,
————————————————–
\sec\theta = \frac{1}{\cos\theta}
\quad\csc\theta = \frac{1}{\sin\theta}
————————————————–
1 + \tan^2\theta = \sec^2\theta\quad\text

\quad 1 + \cot^2\theta = \csc^2\theta\!
————————————————–
\ cos (a+b)=cos a\times\ cos b - sin a\times\ sin b \,
\ cos (a-b)=cos a \times\cos b + sin a \times\sin b \,
————————————————–
\ sin (a+b)=sin a \times\cos b + cos a \times\sin b \,
\ sin (a-b)=sin a \times\cos b - cos a \times\sin b \,
————————————————–
\tan(a+b) = \frac{tan a + tan b}{1-tan a\times\tan b}\ \,

\tan(a-b) = \frac{tan a - tan b}{1+tan a\times\tan b}\ \,

————————————————–

\cot(a+b) = \frac{cot a\times\cot b - 1}{cot a + cot b}\ \,

\cot(a-b) = \frac{cot a\times\cot b + 1}{cot b - cot a}\ \,

————————————————–

\cos 2a=cos^2 a -sin^2 a=2cos^2 a -1= 1 - 2sin^2 a \,

\sin 2a=2sin a\times\cos a \,

————————————————–

\cos^2 a=\frac{1}{2}\ (1+cos 2a) \,

\sin^2 a=\frac{1}{2}\ (1-cos 2a) \,

————————————————–

\ cos a \times\cos b =\frac{1}{2}(cos (a+b)+ cos (a-b))

\ sin a \times\sin b =\frac{1}{2}(cos (a-b)- cos (a+b))

\ sin a \times\cos b =\frac{1}{2}(sin (a+b)+ sin (a-b))

————————————————–

\ cos a +cos b=2 cos\frac{ a+b }{ 2 }\times\cos\frac{ a-b }{2}\ \,

\ cos a -cos b=-2 sin\frac{ a+b }{ 2 }\times\sin\frac{ a-b }{2}\ \,
————————————————–

\ sin a +sin b=2 sin\frac{ a+b }{ 2 }\times\cos\frac{ a-b }{2}\ \,

\ sin a -sin b=2 cos\frac{ a+b }{ 2 }\times\sin\frac{ a-b }{2}\ \,

 

نگین فیروزی

عضویت در کانال تلگرام ریاضی سرا

دیدگاهتان را بنویسید

آدرس پست الکترونیکی شما منتشر نمی‌شود.