به تساوی زیر نگاه کنید :
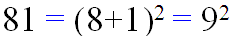
بله 81 برابر است با توان دوم ِ مجموع ارقامش.
آیا اعداد دیگری با این ویژگی وجود دارند؟
به عدد زیر نیز توجه کنید :

حتما ً شگفت زده شده اید ! ادامهی مطلب

به تساوی زیر نگاه کنید :
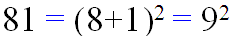
بله 81 برابر است با توان دوم ِ مجموع ارقامش.
آیا اعداد دیگری با این ویژگی وجود دارند؟
به عدد زیر نیز توجه کنید :

حتما ً شگفت زده شده اید ! ادامهی مطلب
قضیه چهار رنگ
قضیه چهار رنگ به صورت ساده این است: یک نقشه داریم میخواهیم ثابت کنیم می توان کشورها را با ۴ رنگ، رنگ کرد به صورتی که هر دو کشور مجاور ناهمرنگ باشند.
این مسله برخلاف ظاهر ساده اش سال ها فکر دانشمندان را به خود مشغول داشت تا در حدود ۱۹۷۶ کی اپپل و و . هیکن بعد از این که ۲۵ سال از عمرشان را وقف اثبات این نظریه کردند، توانستند ثابت کنند که اگر برای حدود ۱۰۰۰۰ نقشه (گراف) ای که لیست شده بودند این کار امکان پذیر باشد آنگاه برای همه ی نقشه ها این کار ممکن است. این تعداد نقشه با کمک کامپیوتر و برنامه ای که آن ها نوشته بودند ، طی روزها تلاش و در طول ۱۲۰۰ ساعت فعالیت سریعترین کامپیوتر زمان خود حل شد. آن ها در واقع در ابتدا قصد استفاده از کامپیوتر را نداشتند ولی ناچار به این کار شدند. بعد کسانی پیدا شدند و گفتند این که نشد اثبات و این دو نفر کلی تلاش کردند که آن ها را قانع کنند که این هم اثبات است و از اثبات ۱۰۰۰ صفحه ای یک قضیه بدتر نیست. ولی هنوز هم دانشمندان در حسرت یک اثبات ساده برای این قضیه هستند. اثباتی که روی کاغذ باشد!
نکته ی دیگر این که این مسئله با کمک نظریه گراف حل شد.
کاربرد فراکتال موسیقی
همواره افرادی بر این عقیده بوده اند که موسیقی از دسته ی علوم ریاضی بشمار میرود و گرچه نوع بیان موسیقی و ریاضی با یکدیگر متفاوت بوده اما روح و حقیقتی که در موسیقی وجود دارد، در ریاضیات قابل مشاهده است؛ بنابراین همواره وجود داشته اند افرادی که بخواهند ریاضیات و موسیقی را به زبان دیگری تعریف کرده و یا از این علوم قدرتمند جهت غنا بخشیدن به دیگری استفاده کنند. آن طور که در تاریخ آمده شروع بررسی موسیقی از دیدگاه ریاضی به یونان باستان بازمیگردد و فیثاغورثیان در پانصد سال قبل از میلاد، اولین افرادی بودند که فواصل موسیقی را متناسب با اعداد بیان کرده و ارتباط موسیقی و ریاضیات را توجیه کردند.
از نه به یک
1x 8 +1 =9
12 x 8 + 2 = 98
123 x 8 + 3 = 987
1234 x 8 + 4 = 9876
12345 x 8 + 5 = 98765
123456 x 8 + 6 = 987654
1234567 x 8 + 7 = 9876543
12345678 x 8 + 8 = 98765432
123456789 x 8 + 9 = 987654321
یکی یکی
1x 9 + 2 = 11
12 x 9 + 3 = 111
123 x 9 + 4 = 1111
1234 x 9 + 5 = 11111
12345 x 9 + 6 = 111111
123456 x 9 + 7 = 1111111
1234567 x 9 + 8 = 11111111
12345678 x 9 + 9 = 111111111
123456789 x 9 +10= 1111111111
پاره خطي را در نظر بگيريد و فرض کنيد که آنرا بگونه اي تقسيم کنيد که نسبت بزرگ به کوچک معادل نسبت کل پاره خط به قسمت بزرگ باشد. به شکل توجه کنيد. اگر اين معادله ساده يعني a2=a*b b2 را حل کنيم (کافي است بجاي b عدد يک قرار دهيم بعد a را بدست آوريم) به نسبتي معادل تقريبا” 1.61803399 يا 1.618 خواهيم رسيد. شايد باور نکنيد اما بسياري از طراحان و معماران بزرگ براي طراحي محصولات خود امروز از اين نسبت طلايي استفاده مي کنند. چرا که بنظر ميرسد ذهن انسان با اين نسبت انس دارد و راحت تر آنرا مي پذيرد. اين نسبت نه تنها توسط معماران و مهندسان براي طراحي استفاده مي شود بلکه در طبيعت نيز کاربردهاي بسياري دارد.