پارادکس جعبۀ برتراند

پاردوکس جعبه‌ی برتراند

جوزف لوئیس فرانسوا برتراند (1900 – 1822) ریاضی‌­دانی فرانسوی بود که در زمینه­‌های نظریه­‌ی اعداد، هندسه تحلیلی، نظریه احتمال، اقتصاد و ترمودینامیک کار می­‌کرد.

برتراند مسائل متنوع و چالش برانگیزی را در ریاضیات مطرح کرده است. یکی از این مسائل که به نام "پارادکس جعبه­‌ی برتراند" مشهور شد، به صورت زیر است:

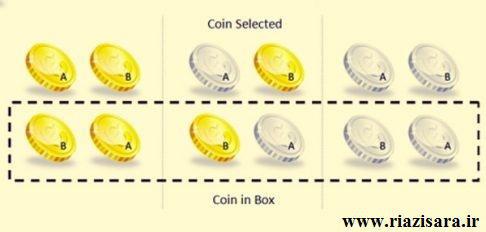
سه جعبه داریم که در یکی از آن‌ها دو سکۀ طلا هست (جعبۀ ط. ط.). در جعبۀ دوم دو سکۀ نقره هست (جعبۀ ن. ن.) در جعبۀ سوم هم یک سکۀ طلا و یک سکۀ نقره هست (جعبۀ ط. ن.). هر جعبه به دو نیمه تقسیم شده است و در هر نیمه یک سکه قرار دارد که می‌توانید هر نیمه را جداگانه باز کنید.

سوال: به طور تصادفی یکی از سه جعبه را انتخاب می‌­کنیم. احتمال اینکه در جعبه‌ی انتخاب شده، دو سکه با رنگ‌های متفاوت وجود داشته باشد، چقدر است؟ (جواب روشن است: یک‌سوم)

حال فرض کنید اولین نیمۀ یکی از جعبه‌ها را که باز کردید متوجه می شوید که داخل آن سکۀ طلاست. در این‌صورت این جعبه یا "ط. ط" است و یا "ط. ن" و در نتیجه، انگار احتمال اینکه این جعبه "ط. ن" باشد یک‌دوم است. به همین ترتیب، اگر در نیمۀ اولِ جعبه‌ای که باز کرده‌اید سکۀ نقره باشد آن‌وقت جعبۀ شما یا "ن. ن" است یا "ط. ن" و در این حالت هم احتمال "ط. ن" بودنِ این جعبه یک‌دوم است. این درحالی است که اولین سکه‌ای که چشمِ‌تان به آن می‌خورد یا سکۀ طلاست یا سکۀ نقره. پس چاره‌ای نیست جز اینکه احتمال "ط. ن" بودنِ هر جعبه‌ای که انتخاب می‌کنید یک‌دوم باشد و نه یک‌سوم!

روشن است که احتمال انتخاب جعبه‌ای که سکه‌هایِ داخل آن هم‌رنگ نباشند یک‌سوم است و لا‌غیر.

 مسأله این است که عیب و ایراد استدلال بالا را پیدا کنیم.

برتراند می‌گوید مغالطه‎ای در کار است و آن اینکه با این فرض که سکۀ نهفته در نیمۀ اولِ جعبه‌ای که انتخاب می‌کنید طلا باشد، احتمالِ اینکه سکۀ نهفته در نیمۀ دیگر طلا باشد با احتمال نقره بودنِ آن به یک اندازه است. اما این فرض درست نیست و احتمال نقره بودنِ سکۀ داخلِ نیمۀ دیگر کمتر است. اگر نیمه­‌ای که انتخاب کرده‌اید "ط " باشد احتمال اینکه جعبه­‌ی انتخابی "ط. ط" باشد، دو برابر احتمالِ آن است که جعبۀ انتخابیِ‌تان "ط. ن" باشد. در نتیجه، دیدنِ اینکه یکی از سکه‌ها طلاست خبر از این می‌دهد که احتمال "ط. ط" بودنِ جعبۀ انتخابی دو برابر احتمال "ط. ن" بودنِ آن است. همین‌طور نقره بودنِ یکی از سکه‌ها خبر از این می‌دهد که احتمال "ن. ن" بودنِ جعبۀ انتخابی دو برابر احتمال "ط. ن" بودن آن است.